Н. Воробьев
|
|
Рис. 1 |
Рис. 2 |
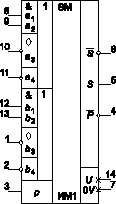
Рассмотрим уравнения и структуры серийно выпускаемых ИС сумматоров. Функциональное обозначение полного одноразрядного двоичного сумматора типа ИМ1 (`80), реализуемого в отечественных сериях 133, К155, КМ155, представлена на рис. 1. Его отличительной чертой является развитая логика на входах разрядов a и b чисел А и В (рис. 2). Структура данной ИС реализуется по следующим уравнениям:
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (5) |
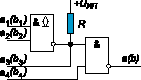
При использовании данной ИС между входами a3 и b3 и источником питания +5 В нужно включить резистор R, сопротивление которого определяется требуемыми динамическими параметрами (типичные значения 15,1 кОм). В дальнейшем на схемах, построенных на этой ИС, резистор опущен.
Реализация прямой суммы и инверсных суммы и переноса в данной ИС обусловлена двумя обстоятельствами: во-первых, задержки распространения логического элемента И-ИЛИ-НЕ меньше, чем у элемента И-ИЛИ, так как последний фактически реализуется по структуре И-ИЛИ-НЕ-НЕ, что позволяет строить параллельные многоразрядные сумматоры с последовательным переносом с относительно небольшими задержками распространения в цепи выходного переноса; во-вторых, используется свойство самодвойственности функций S и P [1].
Наличие входов a1, a2 и b1, b2 позволяет маскировать нулем один разряд, любую группу разрядов или все разряды чисел А и В. Наличие входов a3 и b3 позволяет подключить к ним дополнительную логику, реализованную на элементах, выходы которых выполнены с открытым коллектором. Наличие входов a4 и b4 дает возможность преобразовывать прямые коды многоразрядных чисел А и В в обратный или дополнительный коды, а также строить схемы не только сумматоров, но и вычитателей.
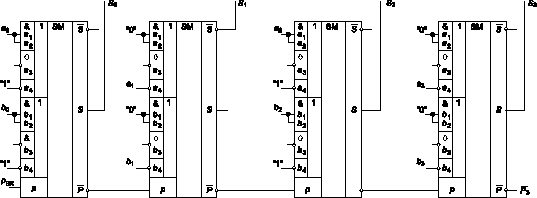
Рис. 3
В качестве примера на рис. 3 показана схема, поясняющая принцип действия 4-разрядного параллельного сумматора с последовательным переносом, в котором использованы ИС типа ИМ1 (133, 155). Разряд a0 числа А подан на объединенные входы a1 и a2, хотя в общем случае на вход a2 можно подать уровень "1" либо использовать его для маскирования. То же можно сказать о разряде b0 числа В. На входы a4 и b4 ИС младшего разряда необходимо подать уровень "1" (выражения (4) и (5)). Младший разряд суммы снимается с выхода S0 сумматора. Несмотря на то, что перенос из младшего разряда поступает с инверсией, мы подаем его непосредственно на вход переноса следующего разряда.
Учитывая свойство самодвойственности, вторые разряды слагаемых a1 и b1 чисел А и В соответственно подадим на входы a4 и b4 ИС, причем на один или оба входа a1, a2 и b1, b2 необходимо подать уровень "0" (выражения (4) и (5)). Так как все три входа этой ИС имеют инверсные переменные, то на выходе реализуется инверсия суммы, однако, если снимать ее с выхода S одноразрядного сумматора, то получим прямое значение разряда S1 суммы. Кроме этого, получится инверсия выходного переноса, но поскольку он снимается с инверсного переноса, то фактически реализуется прямой выходной перенос. Дальнейшие связи остальных разрядов осуществляются аналогично.
Функциональное обозначение двухразрядного двоичного сумматора типа ИМ2 ( `82), реализуемого в отечественных сериях 133, К155, КМ155, представлена на рис. 4.
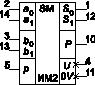
Рис. 4
Структура данной ИС реализуется по следующим уравнениям:(пользователю не доступен) |
(6) |
(структура И-ИЛИ-НЕ-НЕ) |
(7) |
| (8) | |
| (9) |
Выражения (8) и (9) записаны на основании свойства самодвойственности. Инверсия входных разрядов a1 и b1 осуществляется дополнительно встроенными в ИС инверторами.
Как видно из выражений (6)(9), логическая структура этой ИС соответствует двум младшим разрядам схемы (рис. 3), в которых отсутствует входная логика, реализующая выражения (4) и (5).
Быстродействие многоразрядных (n > 4) сумматоров с последовательным переносом, которые можно построить на рассмотренных выше ИС, ограничено задержкой его распространения, так как формирование сигнала переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса младшего разряда не распространится последовательно через все разряды сумматора.
Параллельный перенос в i-ом разряде многоразрядного сумматора определяется как функция разрядов слагаемых i-го и всех предыдущих младших разрядов и входного переноса. Для реализации этого принципа в каждом двоичном разряде сумматора специально формируются два дополнительных сигнала: функция генерации переноса в данном i-ом разряде Di и функция распространения переноса через данный i-ый разряд Fi. Представим перенос из i-го разряда в виде:
Pi = aibi + aipi + bipi = aibi + (ai + bi) pi = Di + Fipi , |
(10) |
где Di = aibi; Fi = ai + bi . Иногда функция Fi реализуется так: Fi = ai Е bi (докажите справедливость последнего выражения самостоятельно). Смысл функций Di и Fi ясен из следующего числового примера:
11 1111 переносы А 01101011 + + В 00100101 S 10010000
Перенос, возникший в младшем разряде D0 = a0b0 = 1.1 = 1, распространяется до разряда с индексом i = 4, а перенос, возникший в разряде с индексом i = 5 : D5 = a5b5 = 1.1 = 1, распространяется до разряда с индексом i = 7.
С учетом вышеизложенного запишем выражения, описывающие структуру 4-разрядного параллельного сумматора с параллельным (быстрым, fast) переносом:
P0 = D0 + F0pвх , |
(11) |
где P0 выходной перенос из разряда с индексом i = 0; pвх входной перенос в разряд с индексом i = 0.
Аналогично
P1 = D1 + F1P0, |
(12) |
Подставив выражение (11) в (12), получим:
P1 = D1 + F1D0 + F1F0pвх, |
(13) |
Выполнив аналогичные процедуры, запишем:
P2 = D2 + F2P1 = D2 + F2D1 + F2F1D0 + F2F1F0pвх , |
(14) |
P3 = D3 + F3P2 = D3 + F3D2 + F3F2D1 + F3F2F1D0 + F3F2F1F0pвх , |
(15) |
В выражениях (12)(13) D1 = a1b1, D2 = a2b2, D3 = a3b3 и F1 = a1 + b1, F2 = a2 + b2, F3 = a3 + b3.
Разряды суммы реализуются так:
S0 = a0 Е b0 Е Pвх |
(16) |
S1 = a1 Е b1 Е P0 |
(17) |
S2 = a2 Е b2 Е P1 |
(18) |
S3 = a3 Е b3 Е P2 |
(19) |
По выражениям (11)(19) выполнена ИС четырехразрядного сумматора с параллельным переносом типа ИМ3, реализуемого в отечественных сериях 133, К155, КМ155. Функциональное обозначение данной ИС приведено на рис. 5. Следует подчеркнуть, что реальная схемотехническая реализация ИС типа ИМ3 осуществляется по преобразованным выражениям (11)(14). Так уравнение (11) с учетом свойства самодвойственности и правила де-Моргана представляется в виде: P0 = a0b0 + (a0 + b0)pвх = a0 + b0 + a0b0pвх.
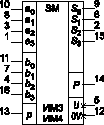
Рис. 5
В настоящее время уравнения, аналогичные (11), (13)(15), реализуют не только внутри структуры сумматора, но и в качестве самостоятельной ИС, причем выражение (15) заменяется двумя выражениями:
D0 = D3 + F3D2 + F3F2D1 + F3F2F1D0 |
(20) |
F0 = F3F2F1F0pвх
|
где D0 функция генерации выходного переноса из четырехразрядной секции; F0 функция распространения переноса через четырехразрядную секцию.
Указанная реализация позволяет каскадировать эти схемы для наращивания разрядности. В качестве примера можно привести ИС типа ИП4 (133, 134, 155, 530, 531, 533, 555, 564, 1531, 1533). Аналогичную структуру имеют ИС типа ИП179 (100, 500, 1500) и ИК03 (585, 589). Такие ИС называют схемами ускоренного переноса (СУП) и применяют совместно с секциями АЛУ и микропроцессоров для повышения быстродействия операционных блоков. Отметим также, что в реальных схемах СУП входные и выходные сигналы могут иметь в качестве активного уровня "0", такой же уровень должны иметь и схемы, которые они обслуживают (АЛУ, процессорные секции).
Рис. 5 представляет также функциональное обозначение четырехразрядного параллельного сумматора с последовательным переносом типа ИМ4, выпускавшегося в составе отечественной серии 134 (снятой с производства в начале 80-х годов). Структура этой ИС полностью напоминает структуру, представленную на рис. 3, в которой отсутствует входная логика, реализующая выражения (4) и (5). Инверсия входных разрядов с индексами i = 1 и 3 осуществляется дополнительно встроенными на кристалле инверторами.
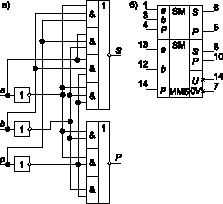
Рис. 6
На рис. 6а и б представлены, соответственно, логическая структура и функциональное обозначение сдвоенного полного одноразрядного двоичного сумматора типа ИМ5 (`183), выпускаемого в отечественных сериях 533, К555. Как видно из рис. 6а, данная ИС выполнена по выражениям:
| (22) | |
| (23) |
при реализации которых используется свойство самодвойственности. Такая структура, даже при наличии инверторов, обеспечивает минимальные задержки распространения сигналов. Данная ИС широко используется при построении быстродействующих суммирующих схем на основе дерева Уоллеса.
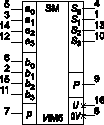
Рис. 7
На рис. 7 представлено функциональное обозначение параллельного четырехразрядного двоичного сумматора с параллельным переносом типа ИМ6 (` 283), выпускаемого в составе серий: 533, К555, КМ555, КР1531. Эта ИС электрически и функционально полностью идентична ИС ИМ3, отличаются они только цоколевкой выводов.
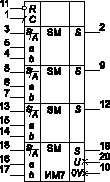
Рис. 8
На рис. 8 представлено функциональное обозначение счетверенного одноразрядного последовательного сумматора/вычитателя типа ИМ7 (`385), выпускаемого в составе серий 533, К555, с общими цепями асинхронного обнуления и синхронной записью (положительным перепадом 01) суммы (результата) и переноса в триггеры хранения. Каждая из четырех секций ИС выполняет сложение/вычитание двух чисел, представленных в дополнительном коде. Числа подаются на входы последовательно младшими разрядами вперед. Результат также получается в дополнительном коде и выдается на выходе последовательно младшими разрядами вперед. Четыре независимые секции работают под управлением собственного сигнала S/A (Subtractor/Adder). Если установлено S/A = 1, то выполняется микрооперация "А минус В", когда S/A = 0, то "А плюс В".
Фактически микрооперация "А минус В" выполняется как "А плюс дополнительный код (-В)". Дополнительный код реализуется как инверсия всех разрядов числа "В плюс 1" в младший разряд. Именно поэтому 0-е значение асинхронного входа сброса R устанавливает триггер суммы в нуль, а триггер переноса либо в 1 (в режиме вычитания), либо в 0 (в режиме суммирования). Положительный перепад синхросигнала C управляет триггерами суммы и переноса в соответствии таблицей функционирования.
В режиме суммирования структура реализует выражения:
| (24) | |
| (25) |
Реально она выполнена с использованием преобразованного выражения (24):
| (26) |
В режиме вычитания структура реализует выражения:
| (27) | |
| (28) |
Инвертирование разрядов числа В в данном режиме осуществляется элементом m2 под управлением сигнала S/A. Напомним, что в режиме вычитания в первом такте триггер переноса установлен в 1.
Таблица функционирования ИМ7
| Режим работы | Входы | Данные в триггере переноса | Выход S после С = | |||||
| R | S/A | a | b | C | перед С = | после С = | ||
| Обнуление | 0 | 0 1 |
х | х | х | 0 | 0 | 0 |
| 1 | 1 | |||||||
| Суммирование | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | ||||
| 0 | 1 | 0 | 0 | 1 | ||||
| 0 | 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | ||||
| 1 | 0 | 1 | 1 | 0 | ||||
| 1 | 1 | 0 | 1 | 0 | ||||
| 1 | 1 | 1 | 1 | 1 | ||||
| Вычитание | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | ||||
| 0 | 1 | 0 | 0 | 0 | ||||
| 0 | 1 | 1 | 0 | 1 | ||||
| 1 | 0 | 0 | 1 | 0 | ||||
| 1 | 0 | 1 | 1 | 1 | ||||
| 1 | 1 | 0 | 0 | 1 | ||||
| 1 | 1 | 1 | 1 | 0 | ||||
Логическая структура одной секции ИС типа ИМ7 приведена на рис. 9. Основное назначение данной ИС построение сумматоров и вычитателей для чисел, представленных последовательными кодами. Она чрезвычайно удобна также для совместного использования с последовательно-параллельным умножителем дополнительных кодов типа 533ИП9 (`384).
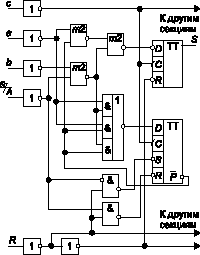
Рис. 9
Один из вариантов группового переноса реализован в четырехразрядном параллельном сумматоре 176ИМ1, К561ИМ1, 564ИМ1 (CD 4008A, B). Функциональное обозначение и логическая структура его приведены на рис. 10а и б, соответственно. Между четырьмя одноразрядными сумматорами внутри ИС реализован последовательный перенос, а выходной перенос P3 реализован как параллельный (выражение (15)).
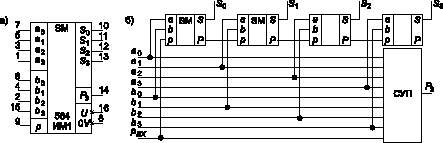
Рис. 10
Сумматоры реализованы и в других, кроме рассмотренных выше, сериях. Например, ИС типа ИМ180 в сериях 100, 500 (MC 10180, MC 10180P) представляет из себя сдвоенный одноразрядный сумматор/вычитатель, способный выполнять четыре микрооперации: "А плюс В", "А минус В", "В минус А", "0 минус А минус В".
Отметим один общий момент, относящийся к способу кодирования разрядов обрабатываемых чисел. Наиболее часто разряды чисел кодируются в положительной логике (1 высоким потенциалом, 0 низким). Какие числа и какой результат будут кодироваться при тех же потенциалах в отрицательной логике? Числа и результат, заданные в одной логике, будут инверсны числам и результату в другой логике (с учетом входного и выходного переносов!)
Рассмотрим числовой пример. Пусть в положительной логике имеем два числа: А = 10 = 1010, В = 11 = = 1011, тогда в отрицательной логике им будут соответствовать числа: А = 5 = 0101, В = 4 = 0100. Сложим и вычтем (с использованием дополнительного кода) и те и другие:
A 1010 A 1010
+ + - +
B 1011 B 0100
Pвх 0 1
---- ----
10101 01111
Накапливающие сумматоры могут строиться двумя способами:
- с использованием счетных триггеров;
- по структуре "комбинационный сумматор плюс регистр хранения".
Первый способ в настоящее время практически не применяется вследствие двухтактности операции сложения, низкой скорости распространения сигналов переноса и сложности управления сумматором.
Во втором случае можно реализовать две схемы:
- с запоминанием результата операции "S: = А плюс В";
- с накоплением результата "S: = S плюс А".
На рис. 11 приведена схема 4-разрядного параллельного накапливающего сумматора, выполненного по структуре "комбинационный сумматор плюс регистр хранения" (на часть схемы, нарисованную штриховой линией пока не обращайте внимания). Число с выхода регистра подается на входы В сумматора, поэтому здесь реализуется микрооперация "S: = S плюс А".
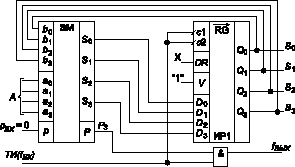
Рис. 11
Если схему дополнить вентилем И, нарисованным штриховой линией, то она может использоваться в качестве "делителя частоты", для которого в общем случае можно записать:
| (29) |
где n разрядность сумматора, А десятичный эквивалент двоичного кода числа А.
Термин "делитель частоты" указан в кавычках, чтобы подчеркнуть тот факт, что выходные импульсы расставляются им неравномерно (равномерная расстановка импульсов обеспечивается только для значений А, являющихся степенью двойки). Временные диаграммы для рассматриваемой схемы при различных значениях А приведены на рис. 12.
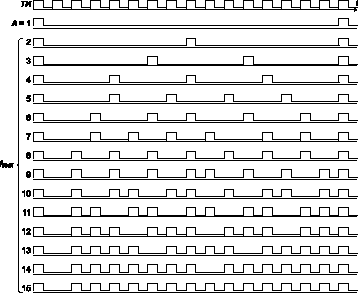
Рис. 12
Кроме использования сумматоров по их прямому назначению, они широко применяются при построении самых различных схем, узлов и операционных блоков. Сумматор является ядром арифметическо-логического устройства (АЛУ), выпускаемого в виде специализированной ИС, причем само АЛУ является ядром процессорных элементов. Чрезвычайно широкое применение находят четвертьсумматоры (элементы "сумма по модулю 2"), реализуемые во многих сериях. Отметим еще несколько примеров использования сумматоров: двоично-десятичные сумматоры, инкременторы и декременторы, цифровые матричные умножители, цифровые фильтры, преобразователи кодов, счетчики и пересчетные устройства, пороговые схемы, линейные цифровые автоматы и др.
Более подробные сведения о рассмотренных и других структурах сумматоров и схемах на их основе можно получить из многочисленных публикаций, в частности [210].
Литература
- Воробьев Н.В. Сумматоры // Chip News. 2000. #2. с.37-40.
- Самофалов К.Г., Корнейчук В.И., Тарасенко В.П. Электронные цифровые вычислительные машины: Учебник. Киев: Высшая школа. 1976. 480 с.
- Ланцов А.Л., Зворыкин Л.Н., Осипов И.Ф. Цифровые устройства на комплементарных МДП интегральных микросхемах. М.: Радио и связь. 1983. 272 с.
- Применение интегральных микросхем в электронной вычислительной технике: Справочник/ Р.В. Данилов, С.А. Ельцова, Ю.П. Иванов и др.; Под ред. Б.Н. Файзулаева, Б.В. Тарабрина. М.: Радио и связь. 1986. 384 с.
- Угрюмов Е.П. Проектирование элементов и узлов ЭВМ.: Учеб. пособие для вузов. М.: Высшая школа. 1987. 320 с.
- Шило В.Л. Популярные цифровые микросхемы: Справочник. М.: Радио и связь. 1987. 352 с.
- Потемкин И.С. Функциональные узлы цифровой автоматики. М.: Энергоатомиздат. 1988. 320 с.
- The TTL Data Book. Volume 1, Texas Instruments, 1989.
- Цифровые интегральные микросхемы: Справочник/ П.П. Мальцев, Н.С. Долидзе, М.И. Критенко и др. М: Радио и связь. 1994. 240 с.
- Пухальский Г.И., Новосельцева Т.Я. Цифровые устройства: Учебное пособие для втузов. СПб.: Политехника. 1996. 885 с.
Тел.: 532 9955
факс: 532 0161


 Сумматоры. Определения, классификация, уравнения, структуры и применение. Часть 2
Сумматоры. Определения, классификация, уравнения, структуры и применение. Часть 2