Четверг, 21 ноября 2024г.

3.7. Флуктуации поверхностного потенциала в МДП-структурах

3.7.1. Виды флуктуаций поверхностного потенциала

Предыдущее рассмотрение электрофизических процессов в МДП-структурах неявно предполагало, что такие параметры, как величина встроенного заряда Q_ox, толщина подзатворного диэлектрика d_ox, концентрация легирующей примеси N_D,A, являются одинаковыми в каждом поперечном сечении МДП-структуры. В связи с этим величина поверхностного потенциала ψ_s, определяемая уравнением электронейтральности

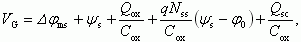   (3.121)

постоянна в каждой точке на поверхности полупроводника вдоль границы раздела полупроводник - диэлектрик.

В реальном случае, вследствие неконтролируемых технологических особенностей обработки поверхности полупроводника и получения подзатворного диэлектрика, величина встроенного заряда Q_ox, толщина диэлектрика d_ox, концентрация примеси N_D,A могут меняться или, иначе говоря, флуктуировать от точки к точке вдоль границы раздела полупроводник - диэлектрик. Согласно уравнению электронейтральности, это вызовет при данном напряжении на затворе V_G различные значения величины поверхностного потенциала ψ_s вдоль границы раздела. Изменение величины поверхностного потенциала ψ_s вдоль области пространственного заряда полупроводника при фиксированном значении напряжения на затворе V_G вследствие флуктуации электрофизических характеристик МДП-структур называется флуктуациями поверхностного потенциала [22].

В том случае, когда пространственный масштаб флуктуаций характеристик МДП-структур велик и обусловлен технологическими причинами, флуктуации поверхностного потенциала называются технологическими. Очевидно, что величина и функция распределения флуктуаций потенциала в этом случае обусловлены конкретным видом флуктуаций того или иного параметра МДП-структур. Крупномасштабные флуктуации потенциала - это флуктуации с размерами, существенно превышающими характерные поперечные размеры МДП-структуры - толщину диэлектрика d_ox и ширину области пространственного заряда W.

В этом случае реальную МДП-структуру можно разбить на малые, параллельно соединенные МДП-конденсаторы, внутри которых значение потенциала ψ_s постоянно. К каждому из таких МДП-конденсаторов применимо уравнение электронейтральности (3.121). Приведенная модель была предложена в работе и получила название конденсаторной модели Гоетцбергера.

В МДП-структурах также существует другой тип флуктуаций поверхностного потенциала, обусловленный дискретностью элементарного заряда. Так, при плотности встроенного в окисел заряда N_ox = 10¹² см^-2 среднее расстояние между зарядами составляет a = 100 A. При концентрации легирующей примеси N_D = 10¹⁵ см^-3 доноры расположены друг от друга на среднем расстоянии a = 1000 A. Очевидно, что в силу случайного характера расположения этих зарядов, их дискретности величина поверхностного потенциала будет также флуктуировать вдоль границы раздела полупроводник - диэлектрик. Флуктуации такого типа характеризуются более мелким масштабом и называются статистическими. К статистическим флуктуациям неприменимо уравнение электронейтральности в виде (3.121).

Технологические крупномасштабные флуктуации поверхностного потенциала можно наблюдать непосредственно в экспериментах со ртутным сканирующим зондом.

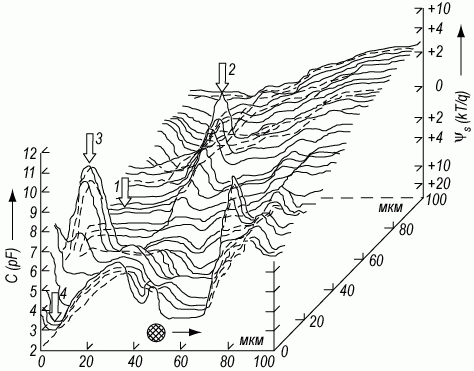
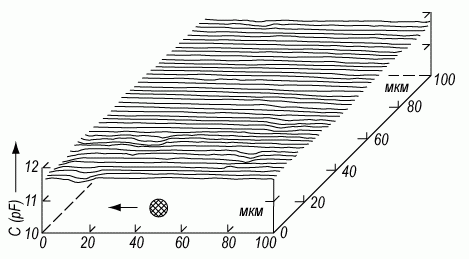
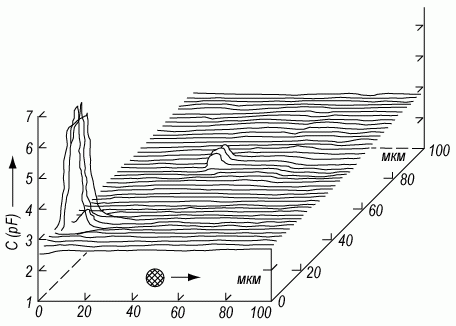
Рис. 3.22. Зависимость емкости МДП-структуры:
а) в обеднении, иллюстрирующая неоднородность поверхностного потенциала; б) в обогащении, иллюстрирующая неоднородность толщины подзатворного диэлектрика d_ox; в) в сильной инверсии, иллюстрирующая однородное распределение концентрации легирующей примеси в полупроводниковой подложке.
Пики соответствуют центрам повышенной (аномальной) генерации.

На рисунке 3.22 приведена в качестве примера зависимость емкости МДП-структуры в обеднении, полученная при сканировании ртутным зондом площадки размером (0,1x0,1) мм² в системе двуокись кремния - кремний. Из рисунка видно, что значения емкости C, а следовательно, и поверхностного потенциала ψ_s, отличаются от точки к точке.Статистические флуктуации в силу их мелкомасштабности нельзя непосредственно измерить и наблюдать в экспериментах с ртутным зондом. Однако они будут проявляться в экспериментах с исследованием процессов переноса в инверсионных каналах вдоль границы раздела полупроводник - диэлектрик, в поведении емкости C и нормированной проводимости G МДП-структур.

Основной задачей при рассмотрении флуктуаций поверхностного потенциала является нахождение функции распределения поверхностного потенциала ψ_s и учет влияния флуктуаций ψ_s на электрофизические процессы в МДП-структурах.

3.7.2. Конденсаторная модель Гоетцбергера для флуктуаций поверхностного потенциала

Пусть флуктуации поверхностного потенциала обусловлены крупномасштабными технологическими флуктуациями плотности встроенного в диэлектрик заряда Q_ox = qN_ox. Толщина подзатворного диэлектрика d_ox и концентрация легирующей примеси N_D,A, как видно из рисунка 3.22а, б, остается постоянной.

Рассмотрим, каким образом можно получить функции распределения P(ψ_s) поверхностного потенциала ψ_s вдоль границы раздела полупроводник - диэлектрик. Пусть N - среднее число заряженных центров на границе раздела полупроводник - диэлектрик, приходящееся на характеристическую площадку α_s. Под характеристической площадкой α_s будем понимать ту минимальную площадь, на которую можно разбить МДП-структуру, чтобы в пределах этой площадки величина поверхностного потенциала была одинакова. Если N - большое число, то функция P(N) будет гауссовской аппроксимацией распределения Пуассона:

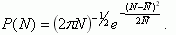   (3.122)

Величина N и плотность заряда Q_ox на площадке α_s связаны очевидным соотношением:

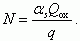   (3.123)

Комбинируя (3.122) и (3.123), получаем для функции распределения плотности заряда P(Q_ox):

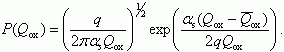   (3.124)

Для функции распределения поверхностного потенциала имеем:

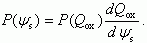   (3.125)

Продифференцировав уравнение электронейтральности в виде (3.121) и учитывая, что 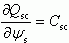, qN_ss = C_ss, а также, что величина dV_G = 0, так как напряжение V_G одинаково для каждой характеристической площадки α_s, получаем:

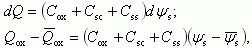   (3.126)

где Q_ox, ψ_s - среднее значение заряда Q_ox и поверхностного потенциала ψ_s.

Подставляя в уравнение (3.125) для функции распределения P(ψ_s) соотношения (3.126) и (3.124), имеем:

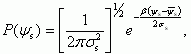   (3.127)

где величина относительной среднеквадратичной флуктуации потенциала 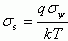равняется:

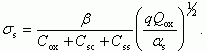   (3.128)

Среднеквадратичная флуктуация потенциала σ_ψ, определяющая отклонение ψ_s от среднего значения ψ_s, будет равна:

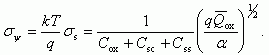   (3.129)

Из соотношения (3.128) следует, что флуктуации потенциала описываются в конденсаторной модели нормальным распределением. Величина среднеквадратичной флуктуации потенциала определяется толщиной диэлектрика d_ox, плотностью поверхностных состояний N_ss, величиной средней плотности заряженных центров Q_ox на границе раздела. Величина ψ_s, входящая в (3.128), в рассмотрении точно не определена. Сравнение теоретического рассмотрения конденсаторной модели с экспериментом по анализу кривых нормированной проводимости G_p/ω показало, что величина площадки α_s равна в области обеднения МДП-структуры квадрату ширины обедненной области (рис. 3.23).

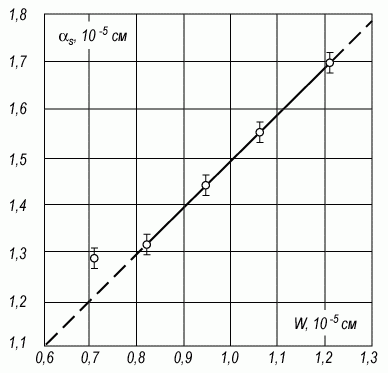
Рис. 3.23. Зависимость площадки α_s от ширины области обеднения W

3.7.3. Среднеквадратичная флуктуация потенциала, обусловленная системой случайных точечных зарядов

Рассмотрим систему зарядов на бесконечной плоскости, координата каждого из которых является случайной функцией. Заряды будем считать малыми и находящимися в узлах со средним расстоянием между узлами ã. Плотность узлов N₀ = ã_-2 значительно больше, чем средняя плотность зарядов Ñ_ox. Вероятность заполнения одного узла α << 1 и равна α = Ñ_ox/N₀.

Потенциал, который создает произвольный узел в некоторой точке A на расстоянии 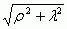от него, будет равен:

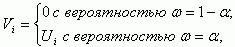   (3.130)

где U_i - потенциал, создаваемый заряженным узлом в точке A,
ρ - расстояние в плоскости от начала координат до заряда,
λ - расстояние от точки A, где ищется потенциал, до плоскости, где расположены заряды.

Средняя величина потенциала V_i, создаваемого i-м узлом, по определению среднего,

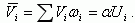   (3.131)

Для расчета среднеквадратичного отклонения запишем:

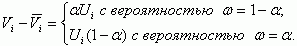
Тогда среднеквадратичное отклонение величины V_i будет равно:

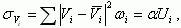   (3.132)

учитывая, что α << 1.

Потенциал U, создаваемый всей совокупностью зарядов на плоскости в точке A с координатами (ρ, λ), будет равен:

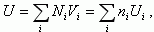   (3.133)

где N_i - число узлов на расстоянии r_i,
n_i - число заполненных узлов на расстоянии r_i.

Учитывая, что заполнение и расположение узлов является случайным, для величины среднеквадратичного отклонения потенциала в точке A с координатами (ρ, λ), обусловленного всеми зарядами, получаем, учитывая (3.133),

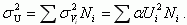   (3.134)

Рассмотрим количество узлов N_i в интервале (ρ, ρ+dρ) около точки A. Оно будет:

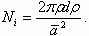   (3.135)

Учитывая определение вероятности заполнения узла α и (3.134), из (3.135) получаем:

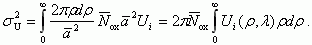   (3.136)

В полученном выражении величина U_i(ρ, λ) имеет смысл потенциала единичного точечного заряда. Таким образом, из (3.136) можно видеть, что величина среднеквадратичной флуктуации потенциала σ_U, вызванной системой точечных зарядов, определяется только их плотностью и потенциалом одного такого заряда.

3.7.4. Потенциал, создаваемый зарядом, находящимся на границе двух сред с экранировкой

Как было показано, величина среднеквадратичной флуктуации потенциала σ_ψ определяется потенциалом единичного точечного заряда при случайном их распределении. В связи с этим интересно рассмотреть зависимость этого потенциала от условий экранировки, которые обычно реализуются в МОП-структурах. Для области слабой инверсии, когда в ОПЗ полупроводника отсутствуют свободные носители, эту область можно рассматривать как диэлектрическую среду с относительной диэлектрической проницаемостью ε_s.

Точечный пробный заряд поместим на границу раздела окисел - полупроводник. Поскольку величины диэлектрической проницаемости полупроводника ε_s и окисла ε_ox различны, необходимо учесть различную поляризацию зарядом этих сред аналогично. И наконец, отраженный в металлическом электроде затвора заряд будет также оказывать свое влияние на поляризацию полупроводника и окисла. Ширину ОПЗ W будем считать существенно большей, чем толщина диэлектрика d_ox, с тем, чтобы исключить экранировку пробного заряда полупроводником. Экранировку потенциала заряда поверхностными состояниями также будем считать отсутствующей.

Поле заряда, расположенного под границей двух диэлектриков

Рассмотрим случай экранировки зарядов на рисунке 3.24. Заряд q₀ расположен в среде I с диэлектрической постоянной ε = ε₁. Требуется найти поле, создаваемое зарядом q₀ в среде II с диэлектрической постоянной ε = ε₂. Оказывается, что в общем случае невозможно подобрать систему зарядов, которые бы давали одновременно правильное значение поля и потенциала одновременно в обеих средах I и II. Поэтому поле в среде I будем искать как поле двух зарядов q₁ и q₂, а поле в среде II - как поле заряда q₃, расположенного в той же точке, что и заряд q₁. Конечно, физически существует только заряд q₀, поле и потенциалы в средах I и II получаются из-за поляризации диэлектриков. Однако оказывается, что подход с введением фиктивных зарядов q₁, q₂ и q₃ удобен и позволяет правильно рассчитывать распределение полей и потенциалов в сложных слоистых системах. Выберем величину заряда q₂ = -αq₁, разницу в величинах ε₁, ε₂ включим в множитель α. Тогда получим выражения для нормальной (E_n) и тангенциальной (E_τ) составляющих электрического поля, изображенных на рисунке 3.24.

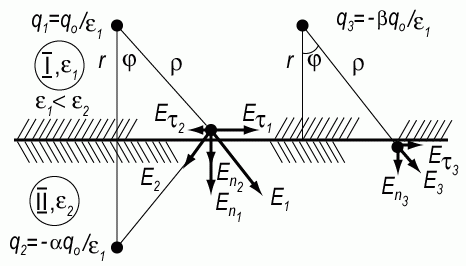
Рис. 3.24. Схема, поясняющая экранировку зарядов границей раздела двух диэлектриков

Сверху границы в области I, где поле определяется зарядами q₁ и q₂, находящимися на на расстоянии τ от границы в среде с диэлектрической проницаемостью ε₁,

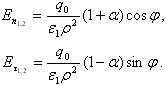   (3.137)

Снизу границы в области II, где поле определяется зарядом q₃ в среде с ε₁,

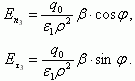   (3.138)

Используя условие постоянства на границе двух диэлектрических сред тангенциальной составляющей напряженности электрического поля E_z1,2 = E_z3 и нормальной составляющей индукции электрического поля ε₁E_n1,2 = ε₂E_n3, получаем:

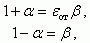   (3.139)

где ε_от = ε₂/ε₁.

Отсюда следует, что

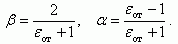   (3.140)

Таким образом, для правильного рассмотрения электрического поля и потенциала, создаваемого зарядом q₀ в среде I с ε₁ и находящегося под границей со средой II с ε₂, необходимо при расчете поля в среде I с диэлектрической постоянной ε₁ пользоваться зарядами q₁ и q₂, расположенными равноудаленно от границы раздела. Величина q₂ = -αq₁, где α приведена в (3.140). Для расчета поля в среде II с диэлектрической постоянной ε₂ необходимо пользоваться зарядом q₃ = βq₁, расположенным на месте заряда q₁ в среде I с диэлектрической постоянной ε₁.

Потенциал заряда в МДП-структуре

Рассмотрим случай, когда точечный заряд находится на границе раздела окисел - полупроводник. Экранировка происходит только затвором структуры (слабая инверсия, низкая плотность поверхностных состояний, стандартное легирование). На рисунке 3.25 изображена возникшая ситуация. Рассмотрим случай, когда нужно сначала рассмотреть поле в окисле структуры. Заряд q, находящийся на границе, отразится зеркально затвором -q, но в этом случае заряд -q - это заряд над границей двух диэлектриков. Из-за поляризации для получения правильного поля в окисле необходимо ввести заряд αq, находящийся по другую сторону на таком же расстоянии от границы раздела. Этот заряд αq в свою очередь снова отразится в затворе и даст заряд -αq. Таким образом, правильное поле в окисле в случае трехслойной МДП-системы получается только при бесконечном наборе зарядов слева и справа от границы раздела.

Для расчета поля и потенциала в полупроводнике все заряды слева на рисунке 3.25 мы должны уменьшить в β раз согласно предыдущему рассмотрению. Следовательно, величина поля и потенциала в полупроводнике МДП-структуры обусловлена суммой зарядов +q и противоположного по знаку -βq, +βαq, -βα²q и т.д., отстоящих на расстояние 2d_ox, 4d_ox, 6d_ox, 8d_ox от границы раздела окисел - полупроводник.

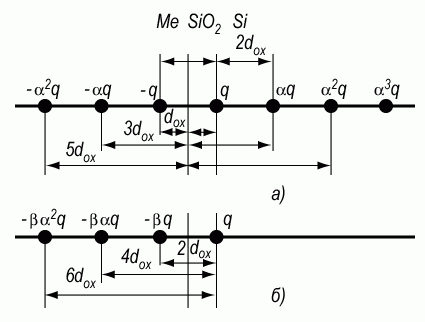
Рис. 3.25. Схема зарядов, необходимая для расчета электрического поля и потенциала МДП-структуры:
а) в диэлектрике; б) в полупроводнике

Условие электронейтральности соблюдено, заряд слева и справа суммарно равны между собой. Поскольку мы предположили, что заряд находится на границе раздела окисел-полупроводник, то

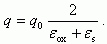
Таким образом, потенциал, создаваемый в полупроводнике точечным зарядом, находящимся на границе окисел - полупроводник при экранировке затвором МДП-структуры, на расстоянии λ вглубь и ρ в плоскости границы раздела можно вписать в виде потенциала распределенного диполя:

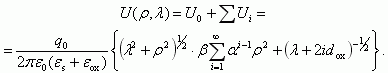   (3.141)

В случае равенства диэлектрических постоянных полупроводника и диэлектрика ε₁ = ε₂ = ε^*, β = 1, α = 0 получаем потенциал простого диполя:

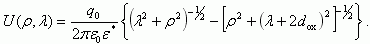   (3.142)

Как следует из соотношений (3.141) и (3.142), различие в потенциалах простого и рассредоточенного диполя будет проявляться при высоких различиях в диэлектрических постоянных окисла и полупроводника, большой толщине диэлектрика d_ox, высоких значениях (по сравнению с толщиной окисла) расстояния вглубь полупроводника λ, где рассчитывается потенциал.

3.7.5. Потенциальный рельеф в МДП-структуре при дискретности элементарного заряда

Для нахождения вида потенциального рельефа в МДП-структуре воспользуемся методом математического моделирования. Для этого, используя датчик случайных чисел, на площадке S, соответствующей в случае МДП-структуры границе раздела полупроводник - диэлектрик, разбрасываются N единичных точечных зарядов со средней плотностью Ñ_ox = N/S. Потенциал каждого заряда рассчитывается с учетом экранировки затвором МДП-структуры по уравнению (3.141). Как и прежде, предполагается, что реализовано условие слабой инверсии или обеднения и толщина подзатворного диэлектрика d_ox меньше ширины ОПЗ.

Для нахождения вида потенциального рельефа потенциалы всех зарядов суммировались и из полученного значения вычиталось среднее значение величины поверхностного потенциала ψ_s, соответствующее квазинепрерывному и равномерному распределению встроенного заряда со средней плотностью Ñ_ox.

На рисунке 3.26 приведена полученная таким образом картина потенциального рельефа. Из рисунка видно, что потенциальный рельеф негладкий, на нем имеются "озера" - участки со значительно меньшим уровнем поверхностного потенциала, "горные хребты" - участки со значительно большим уровнем поверхностного потенциала и, наконец, "долины" - области, где поверхностный потенциал близок к среднему. На приведенной шкале пространственного масштаба видно, что характерный размер областей "озер" и "горных хребтов" составляет порядка 500 Å при толщине диэлектрика d_ox в МДП-структуре d_ox = 50 Å.

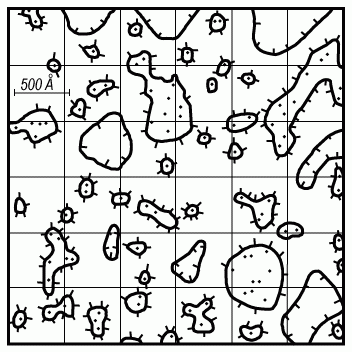
Рис. 3.26. Форма потенциального рельефа в МДП-структуре в области слабой инверсии. Сплошные линии соответствуют отклонению потенциала ψ_s от среднего значения ψ_s на величину среднеквадратичной флуктуации σ_ψ. Точки соответствуют местам расположения зарядов

На рисунке 3.27 приведена зависимость поверхностного потенциала ψ_s от координаты y вдоль границы раздела полупроводник - диэлектрик, рассчитанная для случая, приведенного на рисунке 3.26. Из данного рисунка также видно, что зависимость потенциала ψ_s от координаты является немонотонной функцией.

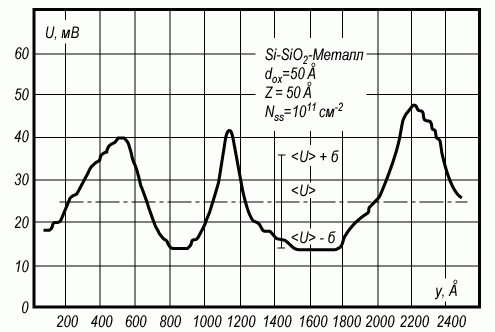
Рис. 3.27. Зависимость потенциала ψ_s от координаты y вдоль поверхности

Таким образом, дискретность и случайный характер расположения в плоскости границы раздела полупроводник - диэлектрик встроенного заряда вызывают флуктуации относительного среднего значения величины поверхностного потенциала.

3.7.6. Функция распределения потенциала при статистических флуктуациях

При рассмотрении флуктуаций поверхностного потенциала вопрос о нахождении вида функций распределения является одним из важных. Поскольку заряженные центры в МДП-структуре дискретны и случайным образом распределены в плоскости границы раздела, то их закон распределения описывается уравнением Пуассона:

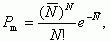   (3.143)

где N - число зарядов, ожидаемое найти на площадке S, Ñ = Ñ_ox·S - среднее число зарядов, находящееся на произвольной площадке S.

Координаты каждого заряда в плоскости ρ_i являются случайной функцией, а общий потенциал от всех зарядов в произвольной точке ОПЗ полупроводника на расстоянии λ будет суммой потенциалов всех точечных зарядов в виде (3.141):

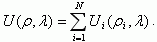   (3.144)

В явном виде совместное решение уравнений (3.141 - 3.144) возможно только при условии λ >> d_ox, ã = Ñ_ox^-1/2.

В этом случае закон распределения потенциала ψ_s описывается гауссовым распределением:

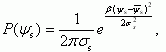   (3.145)

где σ_s - относительная среднеквадратичная флуктуация потенциала ψ_s на расстоянии λ. Поскольку в общем виде соотношения (3.141 - 3.144) не представляется возможным решать в аналитическом виде, для нахождения функции распределения P(ψ_s) использовалось численное моделирование, аналогичное описанному в разделе 3.7.5. Генерируя n раз датчиком случайных чисел координаты всех зарядов, рассчитывалось в произвольной, заранее выбранной точке значение суммарного потенциала. Частота выпадания того или иного значения потенциала соответствовала плотности вероятности.

На рисунке 3.28 показан вид функции распределения поверхностного потенциала ψ_s для МДП-структур с различной толщиной подзатворного диэлектрика в диапазоне d_ox = (50÷1000) Å. Заметим, что функции не нормированы.

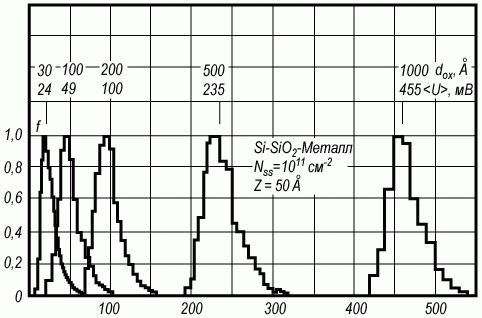
Рис. 3.28. Вид функции распределения f потенциала в МДП-структурах с разной толщиной диэлектрика

Из рисунка видно, что при малых значениях толщины окисла d_ox функция распределения отличается от гауссовой. По мере роста толщины диэлектрика распределение потенциала приближается к нормальному.

На рисунке 3.29 показана зависимость функции распределения от средней плотности заряда Ñ_ox на границе раздела окисел - полупроводник.

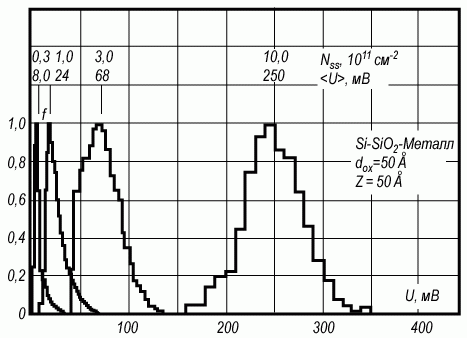
Рис. 3.29. Вид функции распределения f потенциала в МДП-структуре при разной величине плотности заряда

Также видно, что при малых плотностях Ñ_ox функция распределения отличается от гауссовой, по мере роста числа зарядов Ñ_ox распределение потенциала также приближается к линейному.

На рисунке 3.30 показано изменение вида функции распределения по мере приближения к границе раздела окисел - полупроводник. Видно, что средняя часть функции распределения не меняется, но "хвост" функции в сторону вероятности получения больших значений потенциала, по мере приближения к границе раздела, возрастает.

Физическая картина, обуславливающая отличие вида функции распределения поверхностного потенциала ψ_s от нормального распределения, заключается в том, что потенциал кулоновского точечного центра резко зависит от расстояния r при малых значениях r.

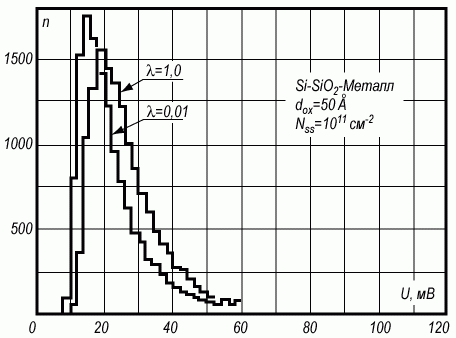
Рис. 3.30. Вид функции распределения f потенциала в МДП-структуре при различных расстояниях λ вглубь полупроводника

3.7.7. Зависимость величины среднеквадратичной флуктуации от параметров МДП-структуры

Как следует из разделов 3.7.3 и 3.7.4, для случая слабой инверсии можно получить зависимость величины среднеквадратичной флуктуации от параметров МДП-структуры. Подставим значение для потенциала единичного заряда U(ρ, λ) в виде (3.142) в выражение (3.136) для величины среднеквадратичной флуктуации потенциала σ_ψ. Для случая ε₁ = ε₂ = ε^* интеграл (3.142) с выражением U(ρ, λ) в виде (3.136) берется в явном виде и получаем:

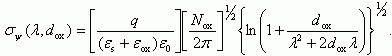   (3.146)

Когда диэлектрические постоянные окисла и полупроводника ε_ox и ε_s сильно отличаются друг от друга, зависимость σ_ψ(λ, d_ox) в аналитическом виде не выражается.

На рисунке 3.31 приведены расчетные зависимости величины средне-квадратичной флуктуации потенциала σ_ψ(λ) при различных толщинах подзатворного диэлектрика. Обращает на себя внимание тот факт, что в случае статистических флуктуаций величина среднеквадратичного отклонения σ_ψ довольно значительно зависит от расстояния λ вглубь полупроводника. По мере уменьшения толщины подзатворного диэлектрика зависимость σ_ψ(λ) увеличивается. Видно также, что чем тоньше подзатворный диэлектрик, тем сильнее экранируются флуктуации и тем меньше величина среднеквадратичной флуктуации потенциала.

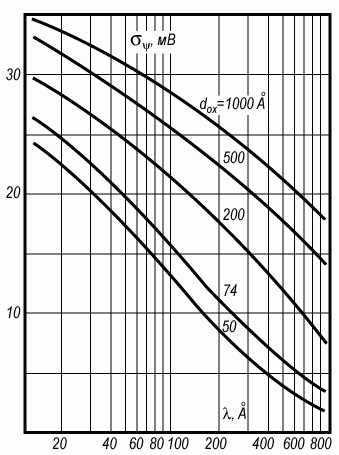
Рис. 3.31. Зависимость величины среднеквадратичной флуктуации σ_ψ от расстояния λ вглубь полупроводника, рассчитанная при различных величинах толщины диэлектрика d_ox

Из соотношения (3.146) следует, что по мере приближения к границе раздела при λ → 0 величина среднеквадратичной флуктуации σ_ψ логарифмически стремится к бесконечности. Этот факт обусловлен тем, что потенциал точечного заряда при r → 0 стремится к бесконечности. Как уже отмечалось в предыдущем разделе, функция распределения потенциала P(ψ_s) в этом случае имеет длинный "хвост" в сторону вероятности нахождения больших значений потенциала. Очевидно, что бесконечных значений потенциала на границе раздела не существует. Физическим ограничением на расстояние λ, на которое носители могут приблизиться к заряженному центру, является его конечный размер. Различные оценки приводят к величине ρ_min = (5÷100) Å в интеграле (3.136) и соответствующей замене нижнего предела интегрирования с нуля на величину ρ_min.

При расчете среднеквадратичной флуктуации σ_ψ(λ, d_ox) с использованием значения потенциала U(ρ, λ) в виде распределенного диполя по уравнению (3.141) и дальнейшего численного расчета интеграла σ_ψ(λ, d_ox) по уравнению (3.136) получено незначительное расхождение между значениями среднеквадратичной флуктуации по сравнению с сосредоточенным диполем только в области малых значений λ. Это позволяет в дальнейшем использовать для расчетов зависимости σ_ψ(λ, d_ox) явное выражение в виде (3.152).

Рассмотрев зависимость величины среднеквадратичной флуктуации σ_ψ от параметров МДП-структуры применительно к переносу заряда в инверсионном канале, Брюс получил аналогичную зависимость в виде:

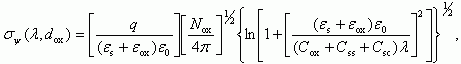   (3.147)

где C_ox, C_ss, C_sc - удельная емкость окисла, поверхностных состояний и полупроводника,
λ - среднее расстояние носителей в инверсионном слое до поверхности.

Выражение (3.147) для σ_ψ было получено Брюсом из решения уравнения Пуассона с использованием функций Грина. Для областей слабой инверсии выражение (3.147) принимает вид:

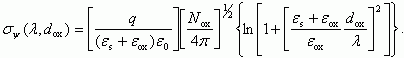   (3.148)

Для случая λ >> d_ox выражения (3.148) и (3.146) дают одинаковое функциональное поведение зависимости σ_ψ ~ λ^-1 и отличаются по величине в 2^1/2 раз. В области малых величин λ ~ d_ox зависимости σ_ψ(λ) также несколько отличаются.

3.7.8. Пространственный масштаб статистических флуктуаций

Рассмотрим, какой характерный пространственный масштаб имеют статистические флуктуации поверхностного потенциала в МДП-структурах. Пусть на границе раздела полупроводник - диэлектрик находятся точечные заряженные центры с поверхностной плотностью N_ox. В силу случайного характера их расположения в плоскости границы раздела распределение зарядов задается уравнением Пуассона. Если мы разобьем плоскость границы раздела на произвольные площадки с размером L, то на одних площадках зарядов будет больше, на других - меньше. Это эквивалентно тому, что наряду с плоскостью, заряженной равномерно, имеется дополнительный набор положительно и отрицательно заряженных площадок. Ситуация будет чем-то напоминать шахматную доску с чередующимися белыми и черными полями. Необходимо рассмотреть, как будет вести себя потенциал такой знакопеременной системы зарядов.

Будем считать за плотность заряда σ на таких площадках избыточную, по сравнению со средней, плотность заряда, обусловленную случайным распределением заряженных центров на поверхности.

Величина σ будет равна:

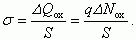   (3.149)

При пуассоновском распределении точечных зарядов на плоскости величина среднеквадратичного отклонения ΔN равна

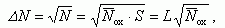   (3.150)

где N - среднее число зарядов на площадке S с размерами L,
Ñ_ox - средняя плотность зарядов на единицу площади.

Рассмотрим, чему равен потенциал заряженной плоскости с линейным размером L. Элементарное интегрирование даст, что потенциал U, создаваемый заряженной плоскостью на расстоянии λ вглубь полупроводника на нормали, проходящей через ее центр, будет:

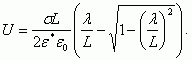   (3.151)

Величина потенциала U₀ на плоскости при λ = 0 будет:

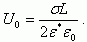   (3.152)

Как следует из уравнений (3.151) и (3.152), величина потенциала U₀ на границе раздела полупроводник - диэлектрик пропорциональна U₀ ~ σL. Тогда с учетом (3.149) и (3.150) имеем для статистических флуктуаций:

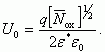   (3.153)

Из соотношения (3.153) следует, что при пуассоновском распределении заряда в плоскости границы раздела полупроводник - диэлектрик величина флуктуации потенциала на поверхности U₀ не зависит от масштаба флуктуаций L, а определяется только средней плотностью заряда Ñ_ox.

Для выявления особенностей экранировки потенциала знакопеременной системы зарядов рассмотрим модельную задачу. Пусть на границе раздела полупроводник - диэлектрик распределен заряд с плотностью σ(x, y), изменяющейся по гармоническому закону:

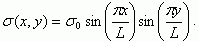   (3.154)

Для нахождения потенциала, создаваемого в полупроводнике такой системой зарядов, запишем уравнение Пуассона в виде:

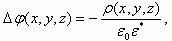   (3.155)

где ρ(x, y, z) - объемная плотность заряда.

Решение уравнения Пуассона приводит к следующему значению потенциала φ(x, y, z):

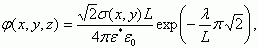   (3.156)

где L - линейный масштаб одной ячейки,
λ - расстояние от границы раздела вглубь полупроводника до точки, где рассчитывается потенциал.

Вследствие экранировки заряда, находящегося на границе раздела полупроводник - диэлектрик металлическим затвором МДП-структуры, за счет сил зеркального отражения в затворе возникает потенциал U_отр, описываемый в полупроводнике соотношением:

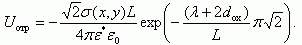
Суммарный потенциал в полупроводнике с учетом экранировки, как показано на рисунке 3.32, будет равен:

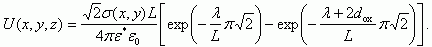   (3.157)

На рисунке 3.32 приведена зависимость потенциала U(x, y, z) от расстояния λ вглубь полупроводника, рассчитанная по уравнению (3.157).

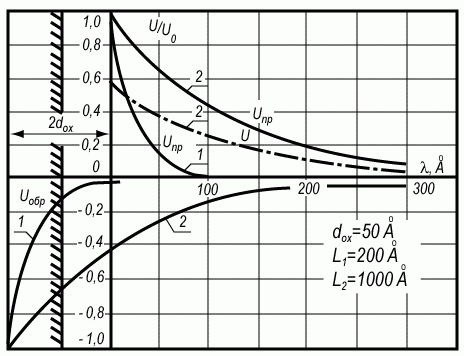
Рис. 3.32. Зависимость потенциала U/U₀ знакопеременной системы зарядов типа "шахматная доска" от расстояния λ вглубь полупроводника с учетом экранировки затвором МДП-структуры

На рисунке 3.33 приведен закон спада потенциала вглубь полупроводника в зависимости от масштаба L. Как следует из этого рисунка, мелкомасштабные флуктуации на больших расстояниях экранируются эффективнее, чем крупномасштабные.

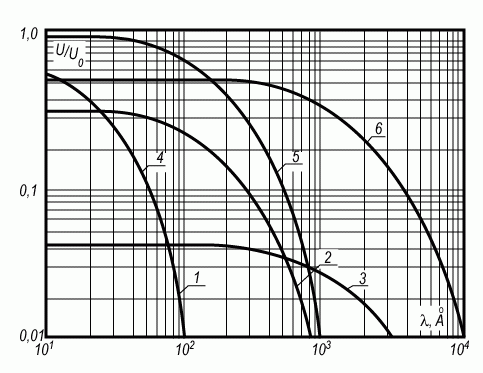
Рис. 3.33. Потенциал U/U₀ системы зарядов типа "шахматная доска" в зависимости от расстояния λ вглубь полупроводника:
d_ox = 50A, 1 - L = 100A, 2 - L = 1000A, 3 - L = 10000A,
d_ox = 1000A, 4 - L = 100A, 5 - L = 1000A, 6 - L = 10000A

На рисунке 3.34 показан характер экранировки потенциала в зависимости от масштаба L при разных толщинах подзатворного диэлектрика d_ox и различных расстояниях λ.

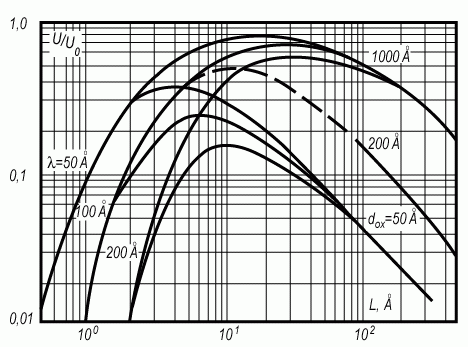
Рис. 3.34. Зависимость потенциала U/U₀ системы зарядов типа "шахматная доска" от размера L при различных толщинах окисла d_ox и расстояниях λ вглубь полупроводника

Видно, что зависимость потенциала U от масштаба L имеет выраженный максимум. Исследование соотношения (3.157) на экстремум показывает, что оптимальная величина масштаба L_опт, соответствующая максимальному значению потенциала (U/U₀)_max, будет равна:

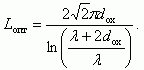   (3.158)

На рисунке 3.35 приведена зависимость масштаба L_опт, рассчитанная по соотношению (3.158) от толщины диэлектрика при разных расстояниях вглубь полупроводника.

При больших значениях толщины диэлектрика оптимальный масштаб имеет размеры порядка толщины диэлектрика L_опт ~ d_ox, при малых толщинах диэлектрика величина оптимального масштаба существенно больше толщины диэлектрика L_опт >> d_ox.

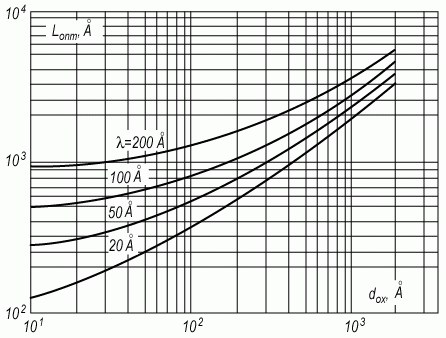
Рис. 3.35. Зависимость оптимального масштаба L_опт, соответствующему максимальному значению относительного потенциала U/U₀, от толщины подзатворного диэлектрика d_ox

3.7.9. Сравнительный анализ зависимости среднеквадратичной флуктуации σ_ψ и потенциала оптимальной флуктуации

Представляет определенный интерес сравнение спада потенциала U(λ), рассчитанного по соотношению (3.157) для флуктуаций различного масштаба L, со спадом величины среднеквадратичной флуктуации σ_ψ(λ). Воспользуемся тем фактом, что для различных масштабов L величина потенциала на поверхности U₀ будет одинакова, как было показано в уравнении (3.123). Будем также учитывать для каждого значения расстояния λ только оптимальные флуктуации, дающие максимальное значение потенциала, то есть флуктуации размером L = L_опт, рассчитанным по (3.158). Величину U₀ выберем для всех случаев такую, чтобы для одной из толщин диэлектрика значения σ_ψ и потенциала U совпали бы при больших значениях λ → ∞.

При других значениях толщины диэлектрика такое совпадение наблюдалось автоматически.

На рисунке 3.36 приведен график потенциала оптимальной флуктуации, рассчитанный подобным образом. Из графика видно, что при больших λ наблюдается совпадение характера зависимости среднеквадратичной флуктуации σ_ψ и потенциала оптимальной флуктуации U от расстояния λ вглубь полупроводника.

Расхождение наблюдается при малых значениях λ, причем с уменьшением толщины диэлектрика d_ox область значения λ, где наблюдается это расхождение, также уменьшается. При значениях λ → 0, то есть при приближении к границе раздела полупроводник - диэлектрик, величина среднеквадратичной флуктуации σ_ψ логарифмически расходится, в то время как потенциал оптимальной флуктуации имеет конечное значение, равное U₀.

Зависимость величины потенциала флуктуации U от масштаба L приведена ранее на рисунке 3.34. При пуассоновском характере распределения точечных зарядов очевидно, что должна наблюдаться минимальная величина масштаба флуктуации, определяемая средним расстоянием между заряженными точечными центрами.

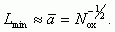   (3.159)

Для Ñ_ox = 10¹⁰см^-2 величина L_min будет порядка 1000A,
для Ñ_ox = 10¹²см^-2 величина L_min будет порядка 100A.

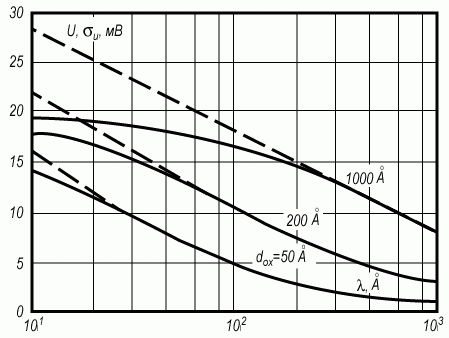
Рис. 3.36. Зависимость потенциала оптимальной флуктуации U₀ и величины среднеквадратичной флуктуации σ_U от расстояния λ вглубь полупроводника для системы случайно распределенных точечных зарядов на границе раздела окисел - полупроводник

Таким образом, дискретность зарядов на границе раздела полупроводник - диэлектрик является физической причиной ограничения минимального масштаба флуктуации. Физическое ограничение максимального масштаба флуктуаций определяется размерами исследуемой МДП-структуры: L_max ≈ L_обр.

Таким образом, на границе раздела окисел - полупроводник возможны все масштабы флуктуаций заряда от L_min до L_max. Но в силу экранировки затвором во флуктуации потенциала дают максимальный вклад такие масштабы, которые удовлетворяют соотношению (3.158). В данном случае МДП-структура выступает чем-то в виде RC-фильтра, который из набора сигналов всех гармоник выделяет преимущественно одну частоту.

При переходе от области слабой к области сильной инверсии начинает играть свою роль экранирование свободными носителями. В некотором смысле это эквивалентно установке и приближению к границе второго затвора со стороны полупроводниковой подложки. Учтем этот факт экранировки следующим образом. Введем расстояние d_nn из условия равенства емкостей области пространственного заряда C_sc и емкости конденсатора с диэлектрической проницаемостью ε_s и расстоянием между обкладками d_nn. Получаем:

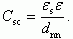   (3.160)

Величина d_nn для области сильной инверсии будет эквивалентна среднему расстоянию свободных носителей в области пространственного заряда до границы раздела полупроводник - диэлектрик. С ростом избытка свободных носителей в инверсионном канале Γ_p,n величина d_nn будет уменьшаться и, как следует из рисунка 3.36, будет происходить экранировка флуктуаций сначала больших масштабов. При этом будет уменьшаться и абсолютная величина флуктуаций потенциала, как видно из рисунка 3.36, и потенциальный рельеф будет становиться все мелкомасштабнее.

Максимальная длина свободного пробега дырок в инверсионных каналах кремниевых МДП-структур, рассчитанная из значения подвижности в максимуме зависимости μ(Γ_p) при температурах T = (77÷350)°К, составляет величину не более λ = (200÷300) A.

Величина линейного масштаба оптимальной флуктуации, как видно из рисунка 3.35, во всех случаях обычно больше длины свободного пробега, в том числе и в МДП-структурах со сверхтонким подзатворным диэлектриком. Этот факт позволяет рассматривать процесс переноса свободных носителей заряда в сложном потенциальном рельефе в инверсионных каналах МДП-структур как процесс "протекания" в случайном потенциальном поле, а не как процесс рассеяния.

Copyright 1997-2024 CHIPINFO

Реклама на сайте >>

Обратная связь >>

Наши сайты:  Приборы   Блог   Справочник   Новости   Форум   Datasheets   News